1.简介

双目相机测距基于双目的视差原理。通过双目相机获取左右两幅图像，通过匹配图像中的特征点，计算特征点在两幅图像中的视差，进而利用三角测量法计算物体的深度信息。

2.概念

2.1.双目相机测距的原理

双目相机模拟人类双眼的视觉系统，由两个相机并排组成，两相机之间的距离称为基线长度（baseline）。测距的关键是计算视差，然后结合几何关系得出深度信息。

2.1.1 基础公式

双目相机具有如下特点：左右两个相机位于同一平面（光轴平行），且相机焦距一致。其原理图如下：

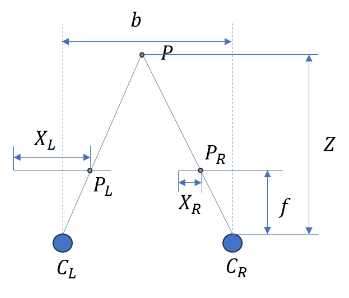
根据平面几何和三角测量公式，有以下关系：

$$ Z=\frac{f\cdot b}{d}=\frac{f\cdot b}{X_R - X_L} $$

其中：

• Z：物体到相机的距离（深度）
• f：相机的焦距（单位与像素匹配，如像素或毫米）
• b：两相机间的基线长度，也就是两个相机水平方向的距离。
• d：图像上的视差(像素单位)

2.1.2.视差的概念

视差（disparity）是指同一物体在两幅图像中的位置差。左右相机拍摄到的图像中，物体的水平位置通常不同：

$$ d=X_R-X_L $$

通过视差，可以确定物体的深度信息。

2.1.3.基线距离的概念

基线距离（Baseline）是双目相机中两个摄像头光学中心之间的水平距离，用于测量物体的深度。它是双目测距的核心参数之一，直接影响测距的精度和范围。

通常，基线距离用符号b表示，单位为毫米（mm）或米（m）。基线的大小由硬件设计决定。

通过双目标定，可以精确计算出两个相机的外参矩阵（即旋转矩阵 RR和平移向量 T）。基线距离为平移向量的模长：

$$ b = \| T \| = \sqrt{T_x^2 + T_y^2 + T_z^2} $$

对于水平排列的相机，通常只有Tx非零，基线距离可以简化为：

$$ b = |T_x| $$

3.计算过程

• 1.通过双目标定等手段得到相机的焦距f，相机的基线距离b，假设已知相机焦距f为5mm，基线距离b为65mm
• 2.两个相机拍摄同时拍照并获取被测物在两个相机中像素位置并做差，假设为100pix

• 3.带入公式可得到

  $$ Z=\frac{5\cdot 65}{100}=3.25m $$