1.景深是什么

在光学成像领域，景深（Depth of Field, DOF）是一个重要概念，它描述了在成像系统中，从最近的清晰点到最远的清晰点之间的距离。本文将深入探讨影响景深的各个方面。

2.影响景深的因素

2.1.弥散圈

当我们对焦时，其实只有一个平面是真正合焦的。这个平面与像平面（可以简单理解为传感器平面）平行。凡是在这个平面之前或者之后的都不是合焦状态。合焦平面上物体某点发出不同角度的光在像平面成像都汇聚于一点，而非合焦物体的某点发出不同角度的光会落在像平面不同点上，形成一个模糊圆，这个圆术语叫做弥散圆（circle of confusion）。

如果弥散圆小到人眼无法鉴别（或者说弥散圆直径小于传感器像元的大小），模糊圆可被视为点的成像，看起来就和对上焦的东西一样清晰，此无法分辨的弥散圆称为容许弥散圆（permission circle of confusion）。在被摄物体（对焦点或合焦平面）前后纵深，有一段距离，其影像在像平面的模糊程度肉眼无法分辨，比较清晰，都在容许弥散圆限定范围内，它们之间距离称为景深。

焦点为光线聚集最紧密的位置，在焦点的前后，光线开始扩散，原来的一个点，就形成了一个扩大的圆斑，这个圆叫做弥散圆，根据人眼的鉴别能力，一定范围内扩散的弥散圆，人眼是不能分辨的，或者认为是可接受的，即依然认为是一个点，此时的弥散圆称为容许弥散圆。

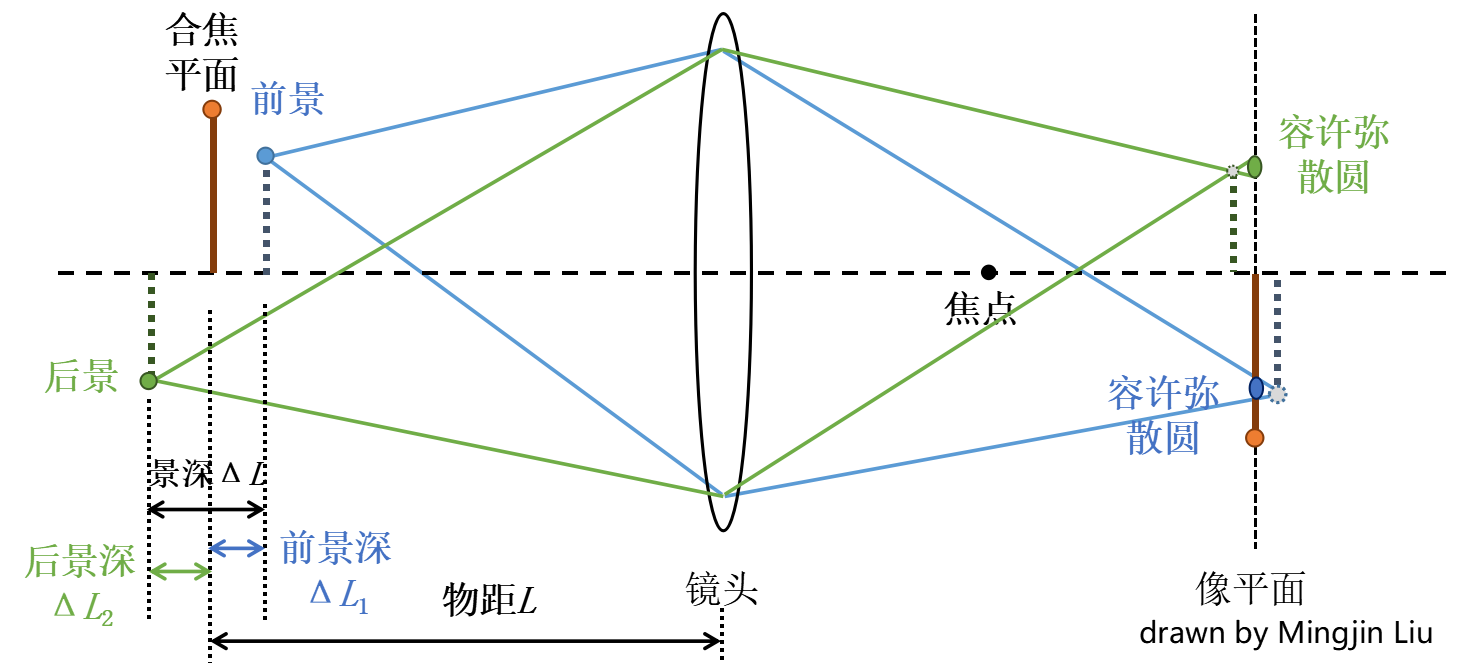
如下图所示，沿光轴方向物方，焦点的前后，各有一个容许弥散圆位置，这两个位置之间的距离就叫做景深，位于这个范围内的被摄物，成像后就被分辨为（或接受为）清晰的。弥散圆所在位置分别称为近点和远点，与物方焦点的距离，分别称为前景深和后景深，后景深大于前景深。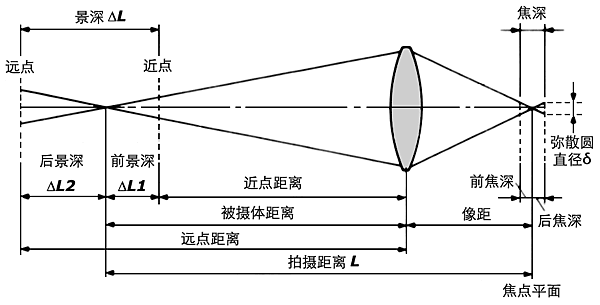

弥散圈直径计算方式1

通常情况下，肉眼分辨率为二千分之一至五千分之一。人眼在明视距离（眼睛正前方30厘米）能够分辨的最小的物体大约为0.125mm。所以，弥散圆放大在7寸照片（这是个常用尺寸）也只能是0.125mm以内，也就是图像对角线长度的1/1730左右。
这个1/1730左右的容许弥散圆大小对于任何大小的底片或者CCD都适用，因为它们放大出来的7寸照片，都可以将弥散圆控制在0.125mm。所以制定的标准就是弥散圆直径=1/1730底片对角线长度。

d为感光元件的对角线长度

$$ 弥散圈直径δ=\frac{d}{1730} $$

如果已知感光元件的宽度 www 和高度 hhh，可以通过以下公式计算对角线长度 d：

$$ d=\sqrt{w^2+h^2} $$

假设已知一个相机感光元件尺寸为36mm x 24mm

则

$$ d=\sqrt{36^2+24^2}≈43.27mm $$

$$ 弥散圈直径δ=\frac{43.27}{1730}≈0.025mm $$

这一公式的逻辑是基于人眼对画面清晰度的容忍度，结合感光元件的尺寸来确定弥散圆的大小

弥散圈直径计算方式2

在数码相机中，弥散圆可以直接设为传感器的像元尺寸，因为它代表了最小的可分辨单位。这种方式适合精确控制景深的情况。

假设像元尺寸为2.8um * 2.8um

即弥散圆的大小为2.8/1000=0.0028mm

2.2.焦距

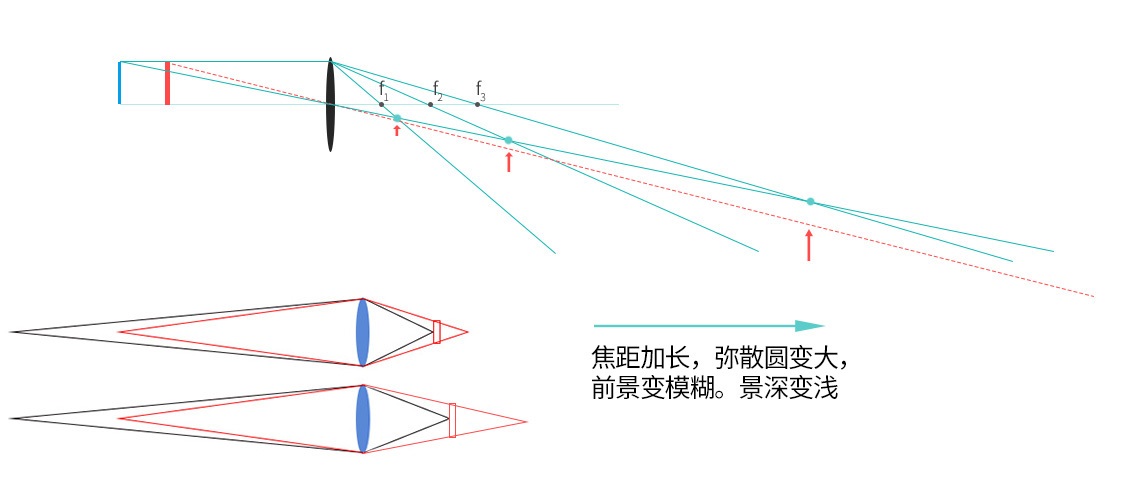
焦距是指平行光入射时从透镜光心到光聚集之焦点的距离，景深与焦距f的平方近似成反比关系。即焦距越长，景深越小(前景深较大)。而且由于平方关系，所以焦距f对景深的影响比光圈N更大；

2.3.光圈

光圈是一个用来控制光线透过镜头，进入机身内感光面光量的装置，它通常是在镜头内。进光量与镜头有效透光孔直径D的平方成正比，与镜头焦距f成反比，D与f的比值称为相对通光孔径，其倒数f/D，称为光圈数，也称F数。光圈F值越小，通光孔径越大，在同一单位时间内的进光量便越多。
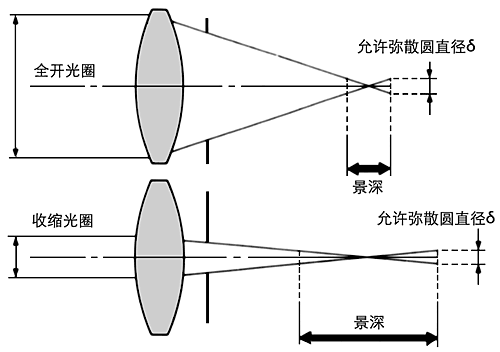
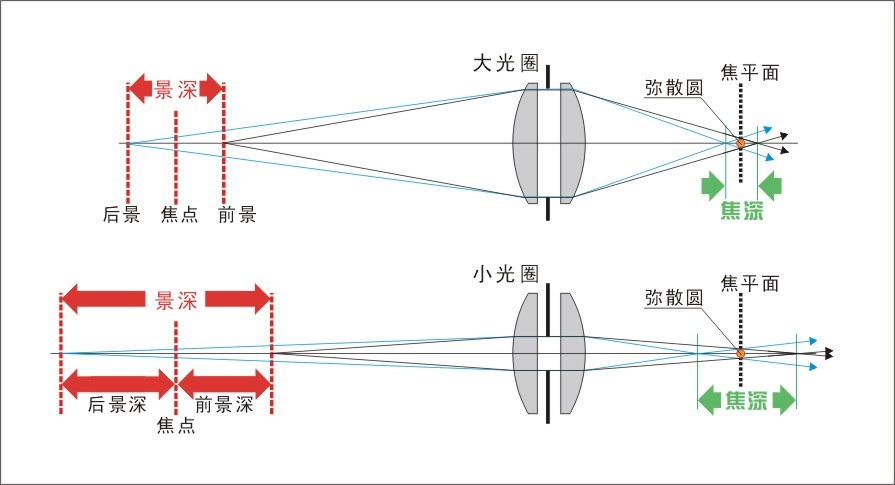
光圈的作用在于决定镜头的进光量，在快门速度(曝光时间)不变的情况下,光圈越大，景深越小（光圈越大，F值越小，进光量越多，有效孔径越大，景深越小）

2.4物距

景深与被摄物距离的平方近似成正比关系。即物距越大，景深越大。同样，由于平方关系，景物距离对景深的影响也比光圈更大。

3.超焦距是什么

当物距远到一定程度后，在一个特定的物距之后一直到无穷远都可以清晰成像，称为超焦距。

4.景深计算方式

F为镜头光圈大小

δ为弥散圈直径

f为镜头焦距

L为拍摄物距

$$ $$

$$ 前景深ΔL1=\frac{FδL^2}{f^2+FδL} $$

$$ 前景深ΔL1=\frac{FδL^2}{f^2-FδL} $$

$$ 总景深 ΔL=ΔL1+ΔL2 $$

$$ 超焦距ΔL=\frac{f^2}{F*δ} $$

前景深是肯定小于后景深的，因为光圈、弥散圈系数和对焦距离都不可能是负数，所以不可能存在前景深小于后景深的情况